CALCULO INTEGRAL

El calculo integral, es una rama de las matemáticas que se encarga del estudio de las integrales y las anti derivadas se emplea mas para calculas aéreas y volúmenes.Fue usado principalmente por, Aristóteles, Descartes, newton y Barrow. Barrow con las aportaciones de newton creo el teorema de cálculo integral que dice: que la integración y la derivación son procesos inversos.

TEÓREMA FUNDAMENTAL DEL CALCULO INTEGRAL 
El teorema fundamental del cálculo integral consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas. Una consecuencia directa de este teorema es la regla de Barrow, denominada en ocasiones segundo teorema fundamental del cálculo, y que permite calcular la integral de una función utilizando la antiderivada de la función al ser integrada.

METODOS DE INTERACIÓNSe entiende por métodos de integración cualquiera de las diferentes técnicas elementales usadas para calcular una antiderivada o integral indefinida de una función.Existen tambien diferentes tipos de métodos de integración, los cuales, son:-Integración directa.-Método de integración por sustitución.-Método de integración por partes.

¿QUIÉN FUE EL CREADOR DEL CÁLCULO INTEGRAL? 
Isaac Newton comparte con Leibniz el crédito por el desarrollo del cálculo integral y diferencial.Leibniz fue el primero en publicar un trabajo sobre cálculo, pero quien primero lo desarrollo fue Newton durante los años 1664 a 1666.Newton abordó el desarrollo del cálculo a partir de: La geometría analítica.Creo el Método de Fluxiones el cual son unas reglas para calcular máximos, mínimos y las tangentes (el cual no fue publicado),desarrollando un enfoque geométrico y analítico de derivadas matemáticas las cuales fueron aplicadas en curvas definidas a través de ecuaciones

Primitivas

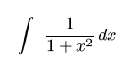 Con el este símbolo estamos representando una función llamada primitiva de la función f(x):=1/(1+x^2) con la propiedad de que su derivada coincide con f. Seguramente usted sabe calcular la primitiva de f ¿verdad? Maxima también la sabe calcular. Utiliza para ello el comando

integrate(1/(1+x^2),x); tiene por primitiva cierta función, que se obtiene haciendo 

No es difícil entender la respuesta de Maxima; ¿está de acuerdo con ella?

Para comprobar si la función arco tangente, que Maxima representa con atan(x), es la respuesta correcta podemos proceder a derivarla.

diff(atan(x),x); tiene por derivada ¿?

Pero también, cualquiera que sea la constante k, se verifica que

diff(atan(x)+k,x); tiene por derivada ¿?

Como esta situación se da siempre, Maxima, de forma implícita, conviene con usted en que eludirá siempre esa constante. Pero... ¿a usted se le había olvidado la constante cuando le preguntamos si estaba de acuerdo con la respuesta de Maxima?

Vamos a complicar un poquito las cosas cambiando de función y tomando f(x):=1/(1+x^4). ¿Sabe calcular la primitiva de f? Le hacemos la misma pregunta a Maxima y obtenemos por respuesta

integrate(1/(1+x^4),x); tiene por primitiva ¿?

Si usted no tiene claro todavía como calcular por sí mismo la nueva primitiva, debería leerse con interés los contenidos teóricos del capítulo «Cálculo de primitivas» relativos a cómo hacer primitivas de funciones racionales, que así se llaman los cocientes de polinomios que puede encontrar en http://ocw.um.es/ciencias/analisis-matematico-i.

Pero volvamos a Maxima. Para saber si se ha equivocado o no lo que tenemos que hacer es derivar el resultado. Usted lo puede hacer «a mano» una vez que entienda el significado de la fórmula anterior que Maxima da como respuesta, y para ello lo único que necesita es saber que sqrt(2) significa raíz cuadrada de 2 y, más generalmente, que sqrt(x) representa la raíz cuadrada de x. ¡Pues manos a la obra! Es un buen ejercicio para usted tomar un papel y derivar la fórmula que Maxima nos ha proporcionado para, después de realizar las simplificaciones oportunas, llegar al resultado buscado.

Para Maxima realizar esos cálculos le lleva muy poco tiempo. Pero es que incluso no necesita que le escribamos con detalle la fórmula que tiene que derivar, porque él ya la conoce, es justamente la «última salida» que nos ha proporcionado y como siempre hace la representa con el símbolo % del tanto por ciento; de suerte que el resultado de derivar la última salida

diff(%,x); es ¿?

- ¡Oiga, pero eso no es lo que esperábamos obtener!

- Tiene usted razón. Veamos si Maxima es capaz de simplificar esa endiablada fórmula de su «última salida» utilizando para ello un comando diseñado con esa finalidad

fullratsimp(%); es lo mismo que ¿?

En efecto, Maxima tenía razón y esa era «la» primitiva, claro está, a falta de la constante.

Sería conveniente que usted realizara también esa misma tarea con lápiz y papel. ¡No sea perezoso, le conviene realizarla!

Integrales

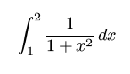 Con este símbolo (que se lee integral de 1 a 2 de 1/(1+x^2)) representamos algo conceptualmente distinto de lo anterior: se trata de calcular el área bajo la curva de ecuación1/(1+x^2) para x entre 1 y 2 cuya gráfica se puede obtener con la siguiente instrucción.

plot2d(1/(1+x^2),[x,1,2]);

La estrategia para calcular el área bajo la curva conceptualmente es la misma que se utiliza para calcular el área de cualquier otra figura geométrica estudiada en el bachillerato: se elige primero la unidad de área (un cuadrado de lado unidad, generalmente) lo cual permite (utilizando la invariancia del área por movimientos rígidos de las figuras y el hecho de que el área de la unión de dos figuras disjuntas es la suma de las áreas de aquellas) asignar áreas a figuras como rectángulos, triángulos, trapecios... y a partir de dichas figuras asignar área a figuras que se puedan descomponer como uniones disjuntas (o al menos sin solapamiento) de figuras cuya área sepamos calcular.

Aunque no es este el momento de entrar en detalles, con los principios anteriores es posible asignar área a rectángulos cuyos lados tienen longitud racional, pero la fórmula del área de un rectángulo, uno de cuyos lados tiene longitud no racional, conlleva un proceso de aproximación sucesiva (o dicho de forma más precisa, de paso al límite) análogo al que vamos a utilizar para calcular el área bajo la curva anterior.

Dividimos el intervalo en dos partes iguales y consideramos rectas secantes a la curva como se muestra en la figura que sigue. Ello determina una poligonal sobre la curva y una colección de trapecios (dos en este caso) cuya área podemos calcular. Visualmente se aprecia que el área bajo la curva no es muy diferente de la suma de las áreas de dichos trapecios no solapados.

f(x):=1/(1+x^2)$ /* Definimos la función f */ n:2$ x(k):=1+k/n$ /* Definimos el número de intervalos, y sus coordenadas */ puntos_particion:create_list([x(k),f(x(k))],k,0,n)$ plot2d([f(x),[discrete,puntos_particion],[discrete,[1+1/n,1+1/n],[0,f(1+1/n)]]],[x,1,2], [legend, "f(x)","", "",""],[style,[lines,2,1],[lines,1,2],[lines,1,2],[lines,1,2]]);

En la fórmula anterior vaya incrementando el valor asignado a n y cerciorese visualmente de que la poligonal se aproxima progresivamente a la curva con la ventaja añadida de que el área bajo la poligonal es facilmente calculable por tratarse de una colección de trapecios (por claridad, sólo aparece pintado el primero de los n trapecios).

Es ahora el momento de calcular la suma de las áreas de dichos n trapecios. Recordemos para ello que el área de un trapecio es el producto de semisuma de las longitudes de sus bases (entendiendo por tales los lados paralelos, en este caso verticales) por la altura (en este caso horizontal de valor 1/n). Así pues la suma de las áreas de los n trapecios

n:10$ /* Fijamos con ello el número de subintervalos que usamos */ sum( (f(1+k/n)+f(1+(k+1)/n))/2 *1/n , k,0,n ),numer; que da como resultado .3412760634002064 para el valor de n

deribadas 

En matemáticas, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.

Un ejemplo habitual aparece al estudiar el movimiento: si una función representa la posición de un objeto con respecto al tiempo, su derivada es la velocidad de dicho objeto. Un avión que realice un vuelo transatlántico de 4500 km en entre las 12:00 y las 18:00, viaja a una velocidad media de 750 km/h. Sin embargo, puede estar viajando a velocidades mayores o menores en distintos tramos de la ruta. En particular, si entre las 15:00 y las 15:30 recorre 400 km, su velocidad media en ese tramo es de 800 km/h. Para conocer su velocidad instantánea a las 15:20, por ejemplo, es necesario calcular la velocidad media en intervalos de tiempo cada vez menores alrededor de esta hora: entre las 15:15 y las 15:25, entre las 15:19 y las 15:21, etc.

El valor de la derivada de una función en un punto puede interpretarse geométricamente, ya que se corresponde con la pendiente de la recta tangente a la gráfica de la función en dicho punto. La recta tangente es a su vez la gráfica de la mejor aproximación lineal de la función alrededor de dicho punto. La noción de derivada puede generalizarse para el caso de funciones de más de una variable con la derivada parcial y el diferencial.

La derivada de una función f en un punto x se denota como f′(x). La función cuyo valor en cada punto x es esta derivada es la llamada función derivada de f, denotada por f′. El proceso de encontrar la derivada de una función se denomina diferenciación, y es una de las herramientas principales en el área de las matemáticas conocida como cálculo infinitesimal. Concretamente, el que trata de asuntos vinculados con la derivada se denomina cálculo diferencial.¹

Integral definida

Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.

La integral definida se representa por .

∫ es el signo de integración.

a límite inferior de la integración.

b límite superior de la integración.

f(x) es el integrando o función a integrar.

dx es diferencial de x, e indica cuál es la variable de la función que se integra.

Propiedades de la integral definida

1. El valor de la integral definida cambia de signo si se permutan los límites de integración.

2. Si los límites que integración coinciden, la integral definida vale cero.

3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].

4. La integral definida de una suma de funciones es igual a la suma de integrales·

5. La integral del producto de una constante por una función es igual a la constante por la integral de la función.

Función integral

Sea f(t) una función continua en el intervalo [a, b]. A partir de esta función se define la función integral:

que depende del límite superior de integración.

Para evitar confusiones cuando se hace referencia a la variable de f, se la llama t, pero si la referencia es a la variable de F, se la llama x.

Geométricamente la función integral, F(x), representa el área del recinto limitado por la curva y = f(t), el eje de abscisas y las rectas t = a y t = x.